Understanding Entropy

Entropy is one of the most thought provoking and complicated concepts of physics. While being simple enough it hides a level of complexity that leaves people around the world scratching their heads.

Today we are gonna talk about Entropy, what in the world does it actually mean. The misunderstanding of the concept of disorder and how Entropy defines the world around us. Not only defines the state but also holds an importance in the future of our Universe itself.

“ Thermodynamics is the only physical theory of universal content concerning which I am convinced that, within the framework of the applicability of its basic concepts, it will never be overthrown.”! Albert Einstein

Let's do some time travel to understand the concept of Entropy. Trust me I will try to make the journey interesting.

Great Scott! Let's sit in our DeLorian (Time Machine)

Entropy through the years

Thermodynamic definition of Entropy

Alright, looks like we have traveled back in the right time. Its Early 1800s, Napoleon Bonaparte is rising as a great leader in France after the infamous French revolution. And one person who recently resigned from position of Napoleon's Minister of War is working on a paper which he called Principes Fondamentaux de l'Equilibre de Mouvement (Fundamental Principles of the Equilibrium of Movement). An enigamtic philosopher and a successful military leader Carnot was the reason Napoleon was successful (known as Organizer of Victory).(C. C. Gillispie, Carnot, Lazare Nicolas-Marguerite, Dictionary of Scientific Biography. Vol. III Page 70).

Published in 1803 the paper talks about one of the first (incomplete) statement of law of conservation of Energy. He says in any natural process there exists an inherent tendency towards the dissipation of useful energy .

Carnot Engine

Sadi Carnot's piston-and-cylinder diagram from 1824

Around two decades later. His son Sadi Carnot, used the same concept to describe an ideal reversible engine and gave his famous Carnot Engine argument. He proposed an ideal reversible steam engine that undergoes a cycle (which we now call Carnot's Cycle -see below ) such that there is no other engine that is more efficient than Carnot's Engine. Reflections on the Motive Power of Fire by Carnot Translated by R.H.Thurston (link)

Carnot's theorem is a formal statement of this fact: No engine operating between two heat reservoirs can be more efficient than a Carnot engine operating between the same reservoirs.

\[{ \eta ={\frac {W}{Q_{H}}}=1-{\frac {T_{C}}{T_{H}}} \text{ ; (1)} } \]

Any basic Undergraduate thermodynamics textbook have the proof for Carnot's theorem. Another statement of the theorem is : All reversible engines operating between the same heat reservoirs are equally efficient. Another interesting point that we can note is the efficiency of heat engine depends only on the temperature of the source and sync. As can be seen in equation 1.

Carnot's Cycle Depicted in a P-V Diagram

But we still don't have the concept of Entropy and the name.

Clausius defining Entropy

Die Energie der Welt ist constant. Die Entropie der Welt strebt einem Maximum zu.** The energy of the world is constant. The entropy of the world tends towards a maximum.**

~ Rudolph Clausius .The “world” here refers to the universe as a whole. This is the way Clausius gave a summary of the first and second laws of thermodynamics. German from Clausius, conclusion of 'Ueber verschiedene für die Anwendung bequeme Formen der Hauptgleichungen der mechanischen Wärmetheorie' in Poggendorff’s Annals of Physics (1865)‚ 125, 400

Alright let's take our Time machine to 1850 Berlin, Germany where Rudolph Clausius is teaching as a professor at Royal Artillery and Engineering School in Berlin. It was here when he published his most famous paper, Ueber die bewegende Kraft der Wärme ("On the Moving Force of Heat and the Laws of Heat which may be Deduced Therefrom") (On the Moving Force of Heat and the Laws of Heat which may be Deduced Therefrom London, Edinburgh and Dublin Philosophical Magazine and Journal of Science 1851 (link )

In the paper Clausius provided a correlation of heat transfer and work. He writes:

In all cases where work is produced by heat, a quantity of heat proportional to the work done is expended; and inversely, by the expenditure of a like quantity of work, the same amount of heat may be produced

He later on concluded his work in another paper written in 1854 titled (In English in 1856. ( Clausius, R. (August 1856). "On a Modified Form of the Second Fundamental Theorem in the Mechanical Theory of Heat"): "On a Modified Form of the Second Fundamental Theorem in the Mechanical Theory of Heat"

Second fundamental theorem now famously called as Second Law of Thermodynamics was written in this paper as:

"Heat can never pass from a colder to a warmer body without some other change, connected therewith, occurring at the same time "

In the paper Clausius derives that no matter what path we take in a reversible cyclic process. (See P-V diagram above) the ratio of change in heat to the temperature is always zero. i.e. and for an irreversible process it's always less than 0.

\[ \oint \frac{\delta Q}{T} \leq 0 \]

This is famously known as Clausius Inequality

Note: If someone is being adventurous you can read the 1856 paper and see that the T in above formula was actually just a function f(T) and he later shows it to be absolute temperature.

Let us travel 11 years further in Zurich, Switzerland. It was here employed as a professor of Physics in ETH Zurich that Clausius gave the concept and coined the term Entropy.

Clausius Naming Entropy for the first time in The Mechanical Theory of Heat – with its Applications to the Steam Engine and to Physical Properties of Bodies. London: John van Voorst.

\[\Delta S \ge \int \frac{\delta Q}{T}\]

uThis is the Law of Entropy the final form of Second Law of Thermodynamics. Clausis closes off his Memoir with the statement : Die Entropie der Welt strebt einem Maximum zu. The Entropy of the world moves towards a maximum.

And that's the story of thermodynamic definition of Entropy.

Entropy: A Statistical Approach

Boltzmann's grave with famous Entropy relation inscribed on it.

Understanding basics of Statistical Mechanics

For understanding Boltzmann's definition of Entropy we need a small refresher on Statistical Mechanics. Before traveling further in time let's stop in a classroom and discuss it. I will try to make things as simple as possible.

Systems involving 1 degree of Freedom(DoF), like a bead moving in a linear thread were easy to solve with classical mechanics. Even system involving 2 bodies was easily resolved to 2 DoF and solved analytically. But when talking of realistic systems like a gas contained inside a volume the DoFs increase monumentally. For N gas particles confined in a volume (like a glass of water) there are 3N DoFs where in any realistic system N is around the Avogadro Number ($10^{23}$) which even the most sophisticated super computers can't deal with.

In 19th to early 20th century physics dealt with such large systems using thermodynamics which was a "phenomenological"(based on observing patterns in phenomenon without going into underlying cause) study of astronomically large "Macroscopic" systems in equilibrium.

It was in mid 19th century when Maxwell gave his distribution function in Kinetic Theory of Gas which provides one of the first Statistical Law in physics.

Understanding Microstates and Macrostates

While the macroscopic variables like Energy, Volume, etc do not change for a system in equilibrium there can be small microscopic fluctuations inside the system that may lead to change in configuration of the particles in the system but our total energy of the system remains same. These are called "microstates" of the system.

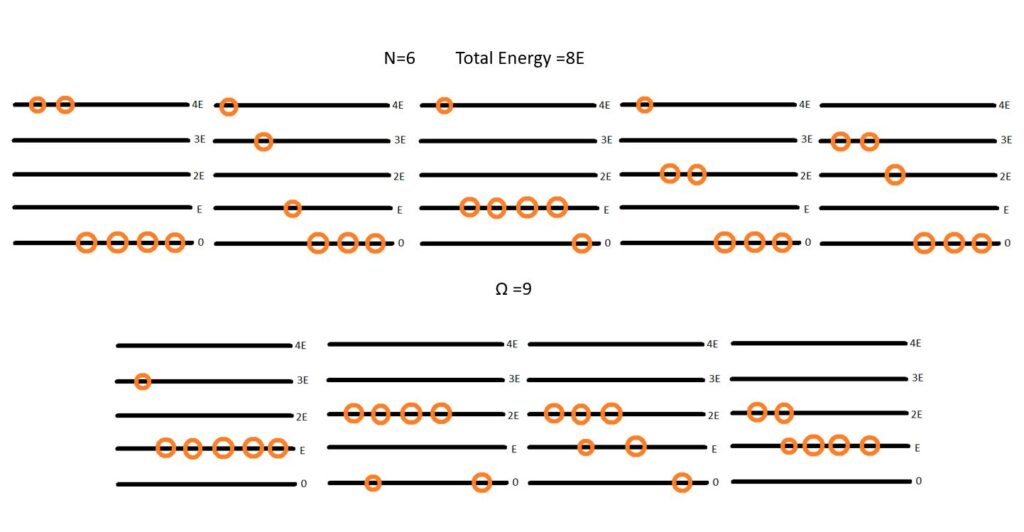
Understanding Microstate and Macrostate (Simple Example)

To understand the concept of Micro and Macrostates let us consider a simple example. Illustrated above we consider a 6 indistinguishable particle system with 5 allowed energy levels (0,E,2E,3E,4E). Basically there are 6 identical balls and 5 shelves in which i can place them.

The Total energy of the system is fixed to be 8E. Now macrostate is defined by the total energy. So all the copies of the system are basically same macrostate.

How do they differ? They differ by their internal distribution. For example we could have a distribution in which two particles are in 4E energy level.

Or we could distribute four of the six particles in 2E level while remaining two in ground level (0).

Its easy to see there are nine such possible distributions. Each such distribution is called a "Microstate" of the system while all of them belong to one macrostate.

Two systems with the same values of macroscopic parameters are thermodynamically indistinguishable. A macrostate tells us nothing about a state of an individual particle.

For a given set of constraints (conservation laws), a system can be in many macrostates.

Statistical Mechanics mostly deals with finding out the probability distribution of such systems.

Bolzmann's definition of Entropy

Let's hop back into our time Machine and travel to 1864 Vienna. A 20 year old student came across Maxwell's paper on The Kinetic Theory of Gases and started working on a series of publication that would lead to a birth of a new branch of physics which we now call Statistical Mechanics.

Beginning in 1866. His first paper was titled, ’On the mechanical meaning of the second law of thermodynamics’, but he reached this objective only in later publications. In 1868 Boltzmann extended Maxwell’s kinetic theory of gases and took the important step of saying that the total energy of the system should be distributed amongst the individual molecules in such a manner that all possible combinations are equally possible.(Now known as one of the postulates of Statistical Mechanics) He later examined the approach to equilibrium according to two ideas, the dissipation of energy and the increase in entropy, and this lead in 1877 to one of the most famous equations of physics: A Very Brief History of Thermodynamics John Murrell (internet archive)

\[S=k_{\mathrm {B} }\ln \Omega\]

Here $ k_{\mathrm {B}} $ is known as Boltzmann constant, commemorating his name. And $\Omega$ is the number of microstates for a corresponding macrostate. In our above example the Entropy for Energy 8E (Macrostate) is given by $S_{8E}= k_{\mathrm {B} }\ln 8$

Note: The form of this equation is consistent with the fact that entropies are additive but probabilities are multiplicative. Note also that as $\Omega$ cannot be less than one, S is always positive.

That's it for our History lesson. Let's apply some of what we have learnt from the greats. Let's travel back to the present.

Gibb's Entropy

The Gibbs entropy is the generalization of the Boltzmann entropy holding for all systems, while the Boltzmann entropy is only the entropy if the system is in global thermodynamical equilibrium. Both are a measure for the microstates available to a system, but the Gibbs entropy does not require the system to be in a single, well-defined macrostate.

This is not hard to see: For a system that is with probability $p_i$ in a microstate, the Gibbs entropy is:

\[S_G = -k_B \sum_i p_i \ln(p_i)\]

and, in equilibrium, all microstates belonging to the equilibrium macrostate are equally likely, so, for N states, we obtain with:

\[\begin{aligned} S_G &= -k_B \sum_i \frac{1}{N} \ln\left(\frac{1}{N}\right) \&= -k_B N \frac{1}{N} \ln\left(\frac{1}{N}\right) \ &= k_B \ln(N)\end{aligned}\]

</td></tr></tbody></table>

by the properties of the logarithm, where the latter term is the Boltzmann entropy for a system with N microstates.

Entropy and Disorder

How would we express in terms of the statistical theory the marvellous faculty of a living organism, by which it delays the decay into thermodynamical equilibrium (death)? … It feeds upon negative entropy … Thus the device by which an organism maintains itself stationary at a fairly high level of orderliness (= fairly low level of entropy) really consists in continually sucking orderliness from its environment.

Erwin Schrödinger

In 'Organization Maintained by Extracting “Order” from the Environment', What is Life? : The Physical Aspect of the Living Cell (1944), 74.

An increase in entropy has often been referred to as an increase in disorder, popular fiction writer often use the word entropy as synonym to chaos. In the quote above you can see how one of the greatest quantum physicist of all time writes Entropy as death itself.

Its quite a spectacle to witness, we humans get seduced by the poetic idea of death. And when a law of physics itself proclaims the death of everything around you, its easy to see how mind can get distracted. This lead to a common misconception though(which is slowly moving away as many textbooks have removed the section of entropy and disorder http://entropysite.oxy.edu/ The 36 Science Textbooks That Have Deleted "disorder" From Their Description of the Nature of Entropy

An example for understanding Order and Entropy

Let us consider another example to discuss order, disorder and Entropy.

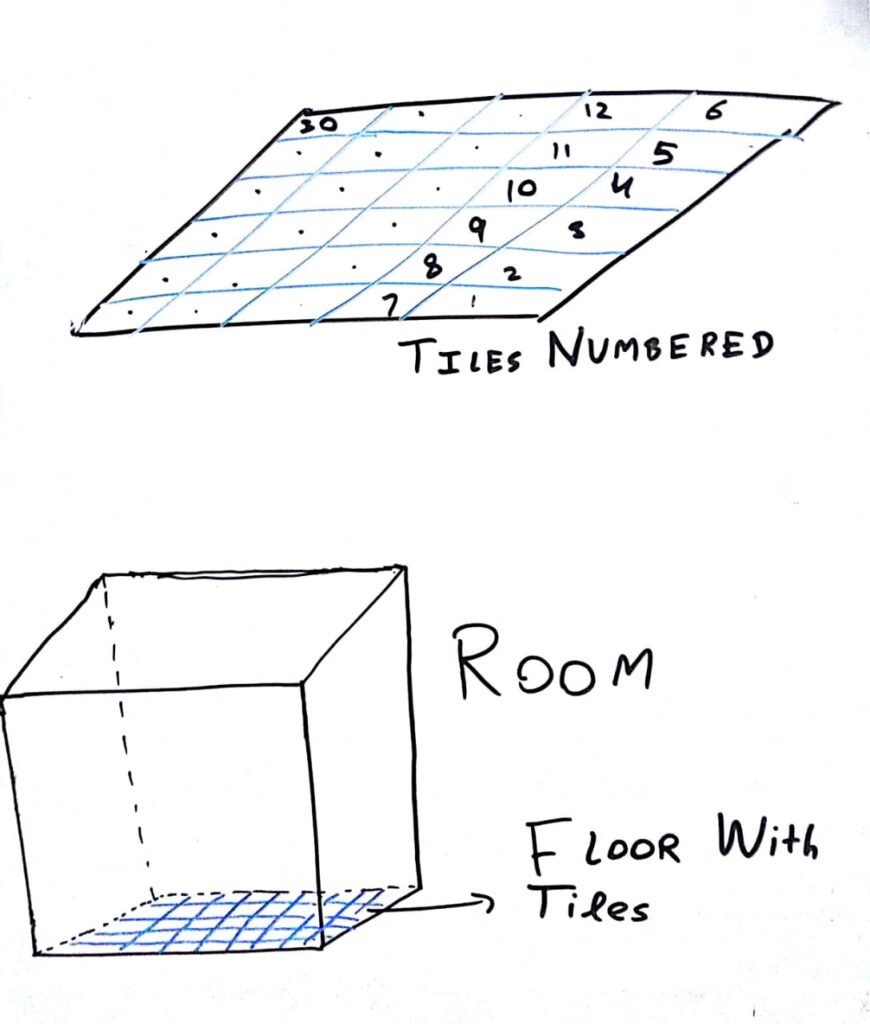
An empty room with floor tiled with indexed tiles.

Let us imagine an empty room with floor tiled as shown in the graphic on left.

Let this floor be divided into 30 equal sized tiles. We can number these tiles from 1 to 30 to make them distinguishable and provide them an index.

Let us say there are 30 balls scattered across the floor. We will consider two different cases.

Case 1: Equal Probability Distribution (Smeared Over)

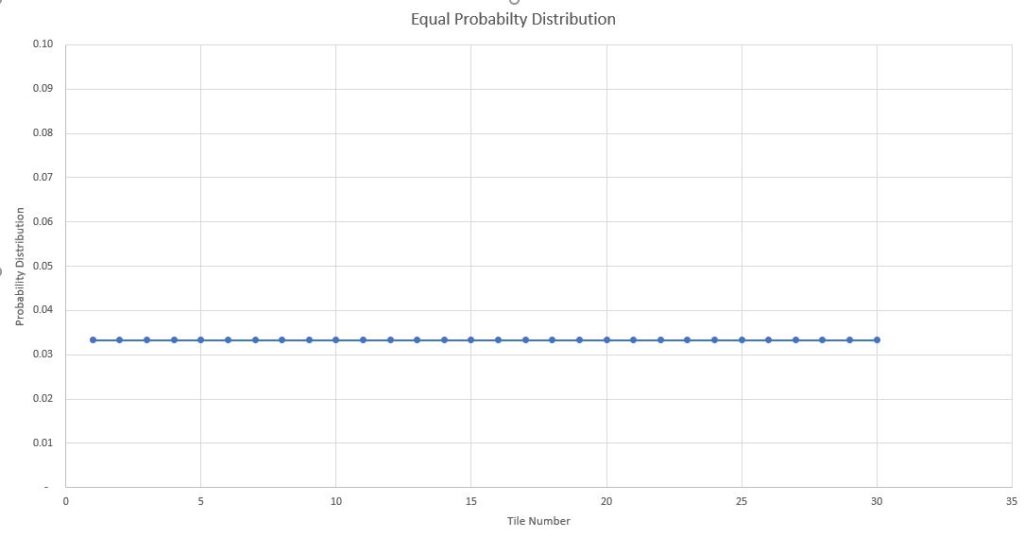
Let all the balls be spread over "smeared over" uniformly across the floor. So that each tile has one ball each. The distribution function for the balls is uniform over all the surface.

That is if you pick up one ball from the floor, probability of it being from first tile is same as the 15th tile and so on.

In this case you can say that your room is not really chaotic. Its completely ordered. In the traditional definition of disorder , the disorder of the room is least in this case.

Probability Distribution plot of Equal likely outcomes

Now let us calculate the entropy for the system using Gibbs Entropy discussed below.

As we can see since the probability is equal for all tiles using normalization $\sum_{i=1}^{30} p_i = 1$ I can write each $p_i$ equal to $\frac{1}{30}$

\[ \begin{align} S_G &= -k_B \sum_{i=1}^{30} \frac{1}{30} \ln\left(\frac{1}{30}\right) \\ &= -k_B 30 \frac{1}{30} \ln\left(\frac{1}{30}\right) \\ &= k_B \ln(30)\end{align} \]

One could prove that maximum entropy is for uniform distribution in simple cases. But for large N and complex probability distribution it is difficult to say. But one thing is sure that for least disorder entropy is zero.

Case 2:

peaked distribution

Let's now say that a toddler or a cat visited and started playing with the balls in the room. After some time the balls will occupy some random distribution and corresponding to that probability distribution one could find out the entropy.

Now let's say the toddler somehow gathers all balls trying to make a fort and put them all along the wall on tile number 12.

Another physical example can be a room with 30 toddlers(imagine the noise in the room) and you put an infinite supply of candy on tile 12. Now if I pick a kid from the room the probability of the kid being from the tile number 12 is unity. (Maximum) while probability that they came from any other tile is zero.

This is what we call a peaked distribution. Where the distribution is constrained to be over only at one point in space.

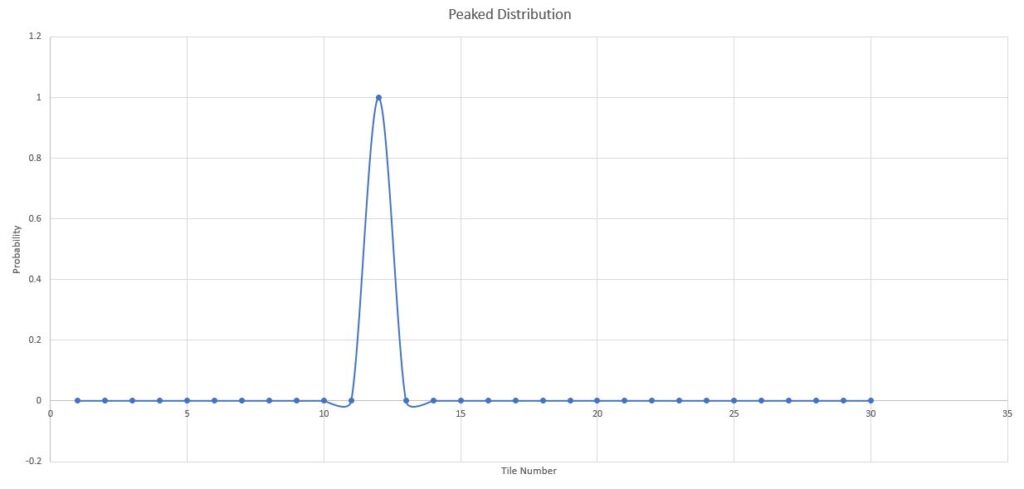
Peaked Distribution - Constrained at one point in space

Now let us calculate the entropy for the system using Gibbs Entropy discussed below.

As we can see since the probability is equal to zero for all tiles except tile number 12. Using normalization we know $p_{12} = 1$ I can write :

\[p_i= \delta _ \delta _={\begin{cases}0&{\text{if }}i\neq j,\\1&{\text{if }}i=j.\end{cases}} \]

\delta _={\begin{cases}0&{\text{if }}i\neq j,\1&{\text{if }}i=j.\end{cases}} $

\[ \begin{align} S_G &= -k_B \sum_{i=1}^{30} p_i \ln p_i \\ &= 0+0+......+ \left\[-k_B \times 1 \times \ln\left(1 \right) \right\] \\ &= 0 \because \ln(1)=0 \end{align} \]

So what we observe here is that entropy is always zero when the distribution is peaked at one point and zero somewhere else. So when our system was disordered and not uniform Entropy turns out to be zero.

So the concept of Entropy being a measure of disorder is wrong. But there's a catch. There is an ambiguity present in the very definition of disorder and order. What I find ordered in the system might look chaotic to another observer. the relative ambiguity is also another reason this definition of Entropy does not hold true in many cases. Also our system needs to be a closed one for even the second law to hold true.

For non isolated system statistical mechanics defines various partition functions and you can deal with them which is beyond the scope of this post. And the connection of Entropy with disorder holds while talking about statistical entropy not the thermodynamic entropy.

Alternative way to look at Entropy

Another way to define Entropy which leads us away from the problem mention above is to leave behind the confusing concept of order and disorder with entropy and rather looking at the Entropy as the measure of lack of information.

There is another branch of science involved here which I won't go into the detail of but in Information theory. In 1948, while working at Bell Telephone Laboratories electrical engineer Claude Shannon set out to mathematically quantify the statistical nature of "lost information" in phone-line signals. He found a quantity that behaved very much like Gibb's Entropy (infact had a covariant form if we replace constant by Boltzmann constant). The quantity is called as Shannon Entropy and is a measure of lack of information.

In case 2 when we had a peaked distribution, we know for sure that ball picked from the room will definitely be from the tile. Thus we know all the information we need for the system and thus have zero entropy.

On the other hand we have in case 1, maximum entropy because of the less information about the system that we know off.

The physical entropy represents a lack of information about a system's microscopic state. It is equal to the amount of information you would gain if you were to suddenly become aware of the precise position and velocity of every particle in the system. Entropy thus is a degree of smoothness of the distribution.

Time,life and Death

Whoa, that was a lot of typing and physics. If you guys are still with me we deserve a cup of coffee or Tea. Let's make one together shall we. Once i mix the milk in my tea, i can't seperate them. This right here is an example of a system going to a state of high entropy. 2nd Law of Thermodynamics state that every close system will ultimately lead to maximum entropy state (As we discussed it before)

The law not only explains the mixing of tea, it also explains why glass shatters, why walls collapse and some believe it also shows us the death of the universe itself.

Death is a morbid topic that has been part of human imagination since a long time. May it be in literature where Dante visits the underworld with Virgil or in cinema. It has been part of our culture, our theologies and thoughts. The morbid curiosity has had many writers writing, philosophers philosophizing and physicists 'physicising'.

“No structure, even an artificial one, enjoys the process of entropy. It is the ultimate fate of everything, and everything resists it.”

― Philip K. Dick, Galactic Pot-Healer

Philip K. Dick talks of Entropy as the harbinger of death and destruction in his novel. Another example can be seen in the writing by John Green (Famous writer of romance novels like The Fault in our Stars, Paper Towns, etc.) cited below.

“Everything that comes together falls apart. Everything. The chair I’m sitting on. It was built, and so it will fall apart. I’m gonna fall apart, probably before this chair. And you’re gonna fall apart. The cells and organs and systems that make you you—they came together, grew together, and so must fall apart. The Buddha knew one thing science didn’t prove for millennia after his death: Entropy increases. Things fall apart.”

John Green Looking for Alaska

Entropy Increases things fall apart. The astronomical leap from the second law of thermodynamics and the destruction of everything might sound poetic, but is it true?

In another great novel of Philip K. Dick (Do Androids Dream of Electric Sheep ) protagonist talks about entropy as the destroyer of even Mozart's music. He writes : "In a way, he realized, I'm part of the form-destroying process of entropy.”

Saying that life and death are consequences of Entropy could be quite a stretch. First of all many scientists have argued that Life (living organisms) show a very structural local complexity. They form Cells, tissues and organs. So you could say that Entropy is decreasing in living systems.

But second law does not allow that. The solution to this problem is simple, you cant consider a living system to be closed. It interacts with outer world. So even if an open system decreases its entropy locally the entropy of the universe still should increase with time.

In this clip from a sci-fi movie Mr. Nobody. The actor talks about Entropy and Arrow of time. It shows us how the notion of Entropy and Disorder has reached the general audience. (Note: This movie is called Science-Fiction for a reason. But we are gonna talk about the same thing it talks about.

Let's take our time machine on one last ride.

Arthur Eddington

Teaching in Cambridge Eddington in 1919 got famous for showing that Einstein's theory of General Relativity was correct by clicking a photograph of a complete solar eclipse and showing light bending through the moon.

Arthur Eddington, (quoted on the left) was very sure of the 2nd Law, so sure that he very famously wrote that it is the "supreme" law of nature.

In 1928 in his book The Nature of the Physical World Eddington introduced the concept of Arrow of time.

The concept basically says that since the entropy of the universe must increase so we can consider an imaginary arrow of time where the entropy of the universe is increasing and that is the only permissible direction we can move in time. We call this direction "the future" He used the word "random" instead of saying entropy directly.

But since the second law does not allow us to move to a lower entropy state. The time only flows in one direction. And we can't actually travel back in time(if the concept is correct)

So actually, the time travel that we have been using to explore the 2nd Law of Thermodynamics and entropy is prohibited by the very same concepts that we have been exploring.

The arrow of time is a concept on which research is presently going on. With some of the finest minds working on it including Late Stephen Hawking.

Here is a video of Brian Cox talking about a concept we discussed today.

Conclusion

Entropy is a difficult concept to wrap your head around. Couple it with some misunderstandings and the use of the word itself in various streams it sometimes might get a bit complicated. We tried to introduce someone with negligible background knowledge to the concepts of Entropy by looking at the evolution of the laws and then used it to explain some of the famous concepts involving Entropy.

A comic strip to end.

title: "Understanding Entropy, Disorder and the Second Law of Thermodynamics" date: "2019-03-28" tags:

"educational"
"entropy"
"mathematics"
"physics"
"thermodynamics"

coverImage: "entropy-4-scaled.jpg"